Brushing Up Calculus - Day 1 of ML

Time spent: 5.5h
Total: 5.5h/10000h

I reflected on my earlier math study sessions and noticed that my attention was spread all over the place. I’m not really sure if anything stuck with me from those sessions.

I figured it’d be good to over basic calculus concepts again to establish a good base. I’ll probably have to do more rigorous study of calculus later on anyway, either for school or for other purposes. Unfortunately, there aren’t many code-based things one can do with the topics gone over today, so I’ll just have to stick to a mathematical approach.

Limits

The limit L of a function $f(x)$ as $x$ approaches $a$ is denoted as $\lim\limits_{x \to a}{f(x)} = L$.
Simply: What value is $f(x)$ getting closer to as $x$ gets closer to $a$? Limits are a very intuitive concept. For example, it would be easy to imply that $f(x) = k$ approaches $k$ no matter what value $x$ approaches, since the value never changes anyway. Hence, $\lim\limits_{x \to a}{k} = k$. Similarly, it would be easy to imply that $\lim\limits_{x \to 2}{x^2} = 4$.

For a limit to exist at $x = a$, the function must approach the same value from both directions. This is where one-sided-limits come into play. When it does, the function is considered to be continuous at $x = a$. A function is considered continous on the interval $[a, b]$ when it has a limit at every value of $x$.

Limits get slightly trickier when there is something like division by zero involved. Algebraic manipulation is often required. There’s also L’Hôpital’s Rule for solving limits with an indeterminate form, like $\frac{0}{0}$ or $\frac{\infty}{\infty}$.

Example 1. Evaluate $\lim\limits_{x \to 2} \frac{x^2 - 4}{x - 2}$.
Solution: $\lim\limits_{x \to 2} \frac{x^2 - 4}{x - 2} = \lim\limits_{x \to 2} \frac{(x - 2)(x+2)}{x - 2} = \lim\limits_{x \to 2} x + 2 = 4$

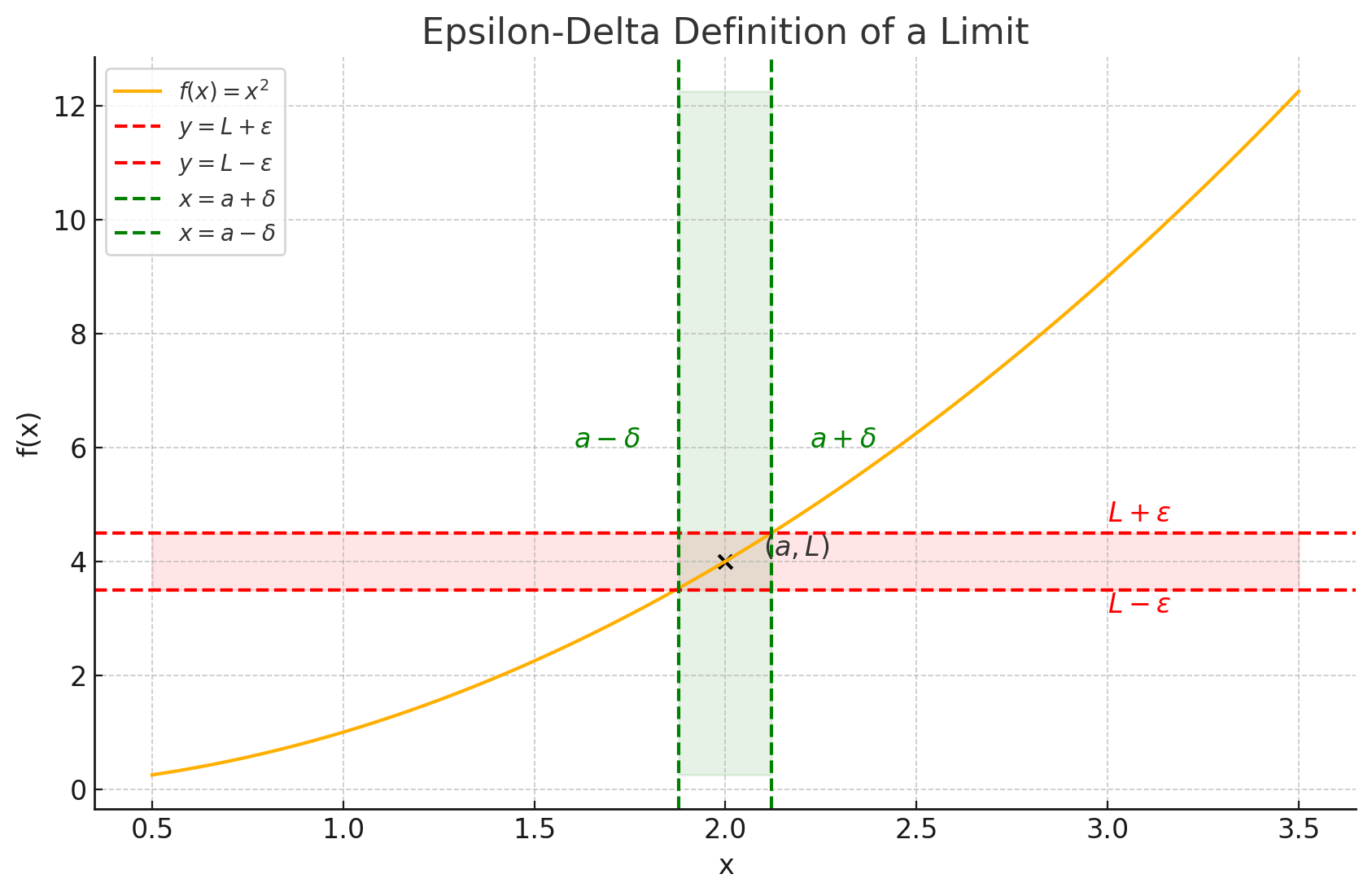
The Formal Definition

A limit is defined precisely when for any $\epsilon > 0$ there is some $\delta > 0$, so that for all $0 < |x - a| < \delta$ we have $|f(x) - L| < \epsilon$.

Whoa! That is a lot of mathematical notation. Let’s break it down a bit. The inequalities can be simplified:

1. The inequality $0 < |x - a| < \delta$ simply states that the distance between $x$ and $a$ is more than $0$ but less than $\delta$. You can look at it like this: $a - \delta < x < a + \delta$.
2. Similarly the equation $|f(x) - L| < \epsilon$ states that the distance between $f(x)$ and $L$ is less than $\epsilon$.

Both of these are conveniently illustrated in the graphic below:

Visualization of the epsilon-delta definition. (Source: ChatGPT-generated matplotlib graphic)

Just imagine $\delta$ and $\epsilon$ getting smaller and smaller, all the way down to infinitesimally small numbers.

Derivatives

The derivative of a function $y = f(x)$, denoted $\frac{d}{dx} f(x)$ or $f'(x)$, is defined as:

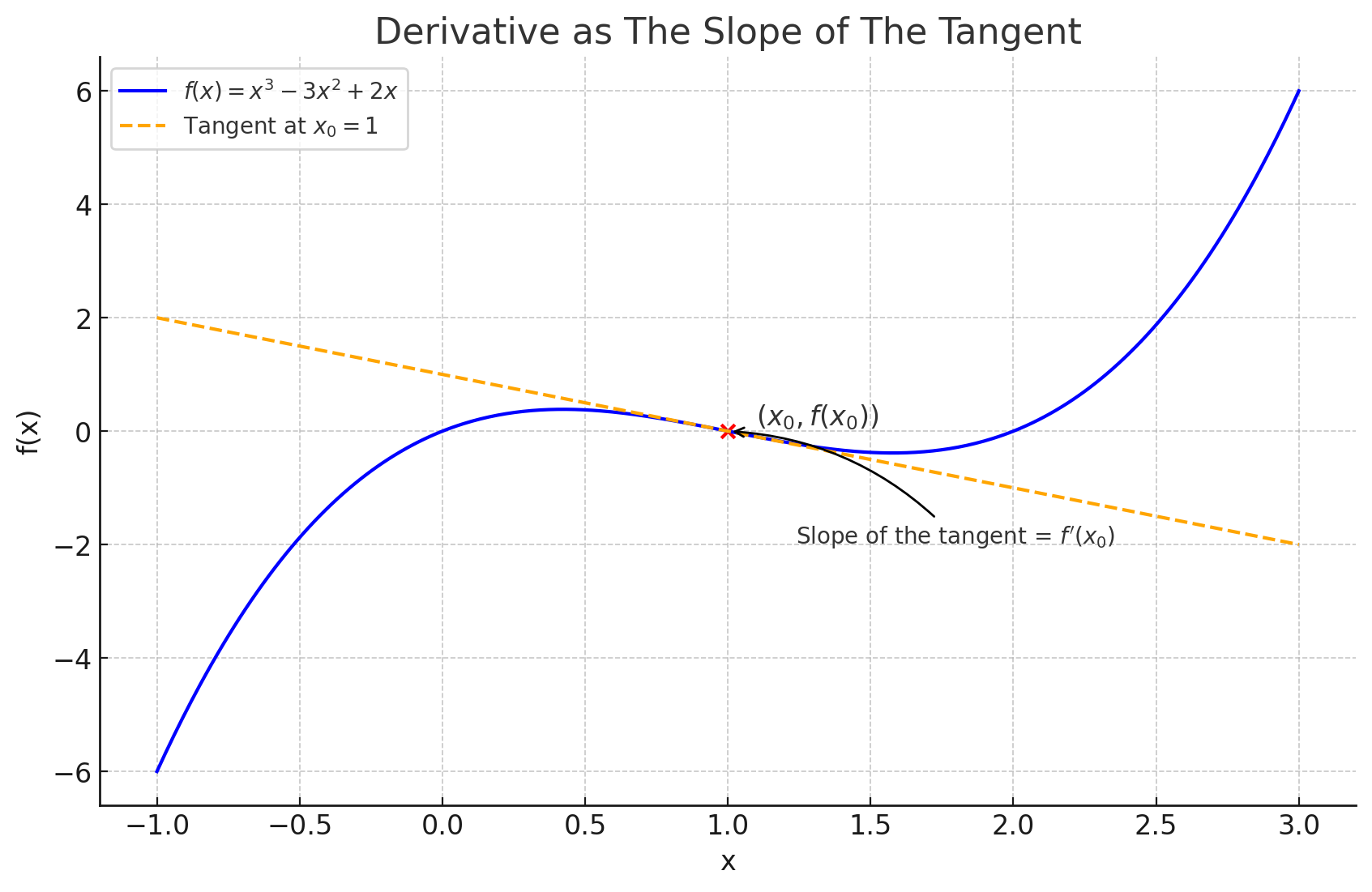
We’ll look into the formal definition in more depth soon. Let’s start with the intuitive definition: the derivative is the slope of the tangent of a function. Essentially, how fast is a function rising at a certain point? This is illustrated in the graphic below:

Intuitive visualization of the derivative. (Source: ChatGPT-generated matplotlib graphic)

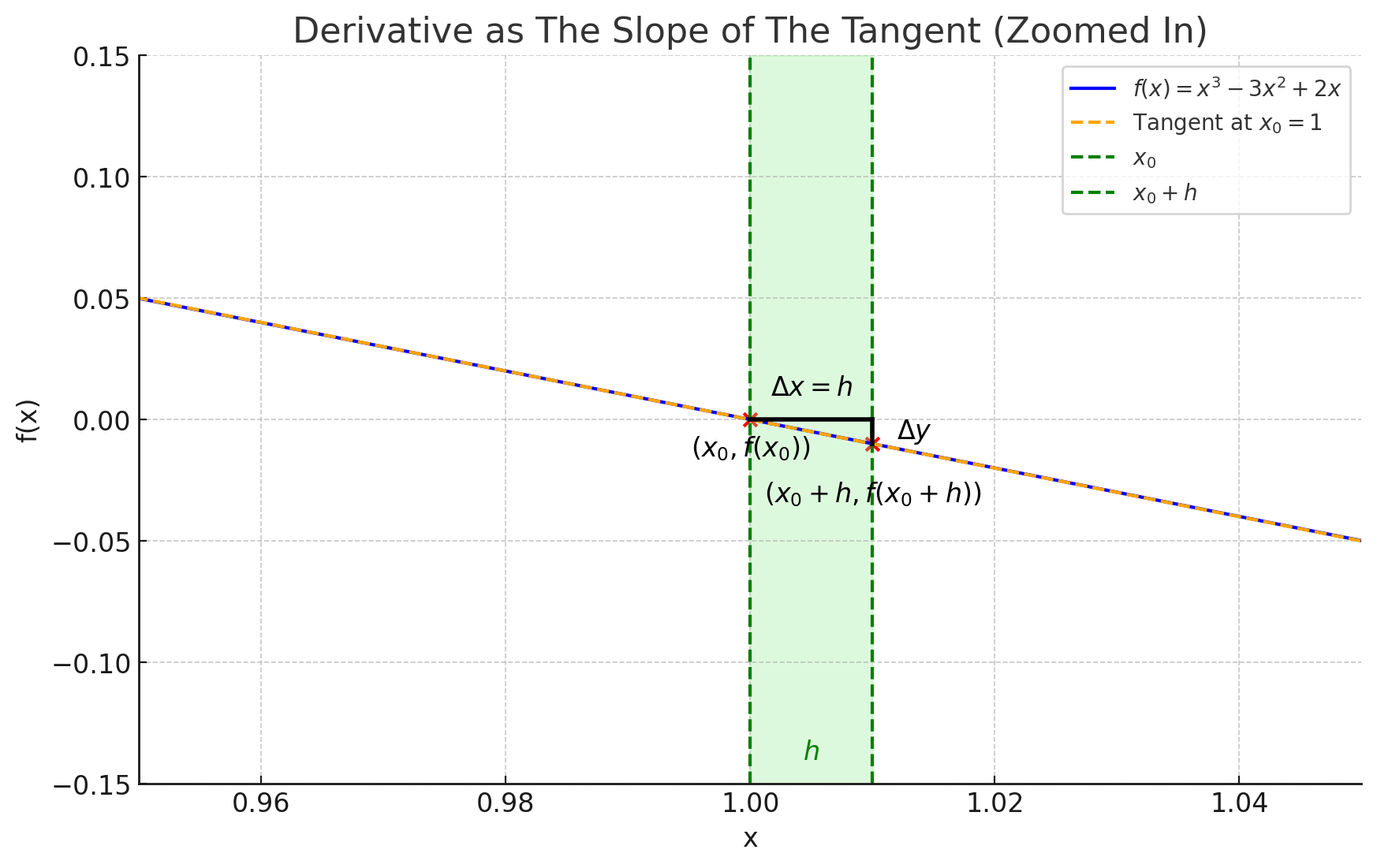
How does the definition of the derivative play into this? In the definition, $h$ is approaching zero, so it should really be treated like it. But it helps to set $h$ to some slightly larger value for intuition purposes. Take a look at the graphic below:

Zoomed-in graphic of the point of the derivative. (Source: ChatGPT-generated matplotlib graphic)

Starting to see a pattern? There are two points: $(x, f(x))$ and $(x + h, f(x + h))$. The derivative is the average rate of change between these two points. Just imagine taking the average rate of change over any normal line - you have $\frac{\Delta y}{\Delta x}$. Here the two points of the line are the points mentioned. $\Delta y$ is just $f(x + h) - f(x)$ and $h$ is the length of the line, or otherwise put, the change of x, $\Delta x$.

In reality however, an image like this wouldn’t be possible since $h$ would be an infinitesimally small number - but the principle stays the same.

Example 1. Evaluate $\frac{d}{dx} f(x)$, where $f(x) = x^2$

Solution:

1. Substitute into the definition: $\lim\limits_{h \to 0} \frac{f(x + h) - f(x)}{h} = \lim\limits_{h \to 0} \frac{(x+h)^2 - x^2}{h}$
2. Simplify: $\lim\limits_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h} = \lim\limits_{h \to 0} \frac{h(2x + h)}{h} = \lim\limits_{h \to 0}(2x + h) = 2x$

Conclusion

I found some notes on derivatives I had written some time ago, they are available here. I probably put too much effort in this one haha. Roughly 6 hours spent learning and writing today. Perhaps I should try measuring my time spent more precisely.